4 📚 Nomenclatura
4.1 Sintaxis
4.1.1 Hola mundo!
Escribamos nuestro primer programa de Python, “¡Hola, mundo!”. Es un programa simple que imprime Hello World! en el dispositivo de salida estándar (pantalla). Para eso se ocupa el comando print().
4.1.2 Variables
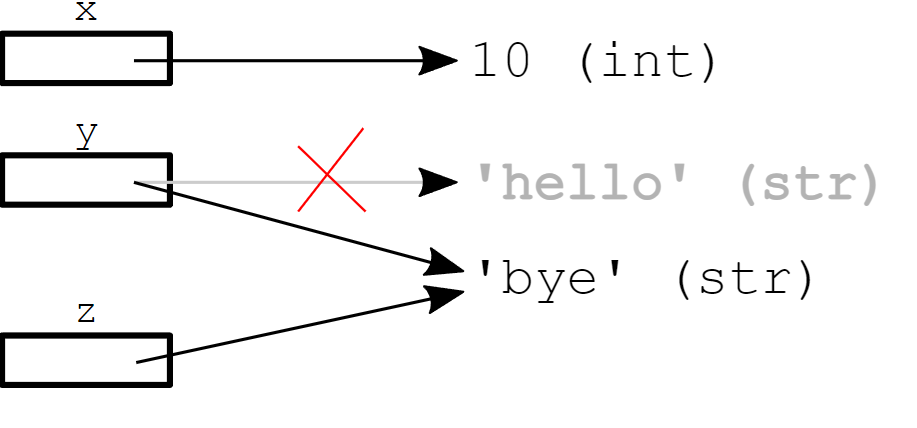
Una variable es una ubicación con nombre utilizada para almacenar datos en la memoria. Una asignación es una sentencia que asocia un nombre al resultado de una expresión.
4.1.3 Imprimir mensajes y variables
La formula para imprimir mensajes y variables es:
print("mensaje_01",variable_01,"mensaje_02",variable_02,...)Existen varias formas de imprimir variables y strings, sin embargo, la que más se destaca es la forma Literal String Interpolation (o también conocido como f-string). La formula es la siguiente:
print(f"mensaje_01 {variable_01} mensaje_02 {variable_02} ...")Observación: Se tratara de trabajar siempre con la forma f-string para ser consistente.
4.1.4 Inputs por el usuario
En Python, puede usar la función input() para tomar la entrada del usuario. Por ejemplo:
# inputs por el usuario
inputString = input('Escriba una oracion:')
print(f'Su oracion es: {inputString}')4.2 Tipos de datos
4.2.1 Enteros, flotantes y números complejos
Python admite enteros, números de coma flotante y números complejos. Se definen como int, float y complex en Python.
4.2.2 Valores lógicos
Los valores lógicos True y False (verdadero y falso) son de tipo bool, que representa valores lógicos.
El nombre bool viene del matemático George Boole, quien creó un sistema algebraico para la lógica binaria. Por lo mismo, a True y False también se les llama valores booleanos. El nombre no es muy intuitivo, pero es el que se usa en informática, así que hay que conocerlo.
4.2.3 Texto
A los valores que representan texto se les llama strings, y tienen el tipo str.
Los strings literales pueden ser representados con texto entre comillas simples o comillas dobles:
4.2.4 Nulo
Existe un valor llamado None (en inglés, «ninguno») que es utilizado para representar casos en que ningún valor es válido, o para indicar que una variable todavía no tiene un valor que tenga sentido.
El valor None tiene su propio tipo, llamado NoneType, que es diferente al de todos los demás valores.
4.2.5 Conversión de tipo
El proceso de convertir el valor de un tipo de datos (entero, cadena, flotante, etc.) en otro se llama conversión de tipo. Python tiene dos tipos de conversión de tipos.
a) Implícita
b) Explícito
Observación: el proceso de transformar string a numeric es correcto cuando lo que está escrito en el string es un número, en caso contrario, nos dará error.
4.3 Operaciones
4.3.1 Operadores aritméticos
Los operadores son símbolos especiales que realizan operaciones en operandos (variables y valores). Hablemos de operadores aritméticos y de asignación en esta parte.
4.3.2 Otros operadores arítmeticos
Potencia
La función potencia de un número entero corresponde a multiplicar \(n\) veces el mismo número. Por ejemplo
\[4^3 = 4*4*4 = 64\]
Cuando el exponente es fracionario, hablamos de raíces. Por ejemplo:
\[4^{1/2} = \sqrt{4} = 2\]
Módulo
Cuando dividimos dos enteros, tenemos una ecuación que se ve como lo siguiente: \[\dfrac{A}{B} = Q \text{ residuo } R,\] donde: * \(A\) es el dividendo * \(B\) es el divisor * \(Q\) es el cociente * \(R\) es el residuo
A veces, solo estamos interesados en cuánto es el residuo cuando dividimos \(A\) entre \(B\). Para estos casos hay un operador llamado el operador módulo (abreviado como mod).
Al usar los mismos \(A\), \(B\), \(Q\) y \(R\) que arriba, tendríamos: \(A \text{ mod } B = R\) (notación). Por ejemplo:
\[\dfrac{13}{4} = 3 \text{ residuo } 1 \textrm{, es equivalente a: } 13 \textrm{ mod } 4 = 1 \]
Redondear
La función incorporada round() toma como argumento un número de coma flotante y retorna un número entero según las reglas del redondeo.
4.3.3 Operadores de asignación
Los operadores de asignación se utilizan para asignar valores a las variables. Probemos algunos operadores de asignación más comunes.
4.3.4 Operadores relacionales
Los operadores relacionales sirven para comparar valores. Sus operandos son cualquier cosa que pueda ser comparada, y sus resultados siempre son valores lógicos.
Operadores relacionales (numéricos)
Operadores relacionales ( string )
4.3.5 Operaciones Binarias
Una tabla de verdad, o tabla de valores de verdades, es una tabla que muestra el valor de verdad de una proposición compuesta, para cada combinación de verdad que se pueda asignar.
| p | q | p ∧ q | p v q | ¬p | ¬q |
|---|---|---|---|---|---|
| T | T | T | T | F | F |
| T | F | F | T | F | T |
| F | T | F | T | T | F |
| F | F | F | F | T | T |
En Python, hay tres operaciones lógicas:
- la conjunción lógica
and(en español: y) - la disyunción lógica
or(en español: o) - la negación lógica
not(en español: no)
| p | q | p and q | p or q | not p | not q |
|---|---|---|---|---|---|
| True | True | True | True | False | False |
| True | False | False | True | False | True |
| False | True | False | True | True | False |
| False | False | False | False | True | True |
4.3.6 Operadores de String
Los operadores de string sirven para poder operar variables tipo str.
4.3.7 Más operadores de String
Existe algunas métodos aplicable a los strings:
Indexaciones
Cada uno de los caracteres de un string (incluidos los espacios) tiene asignado un índice. Este indice nos permite seleccionar su carácter asociado haciendo referencia a él entre corchetes ([]) en el nombre de la variable que almacena la cadena.
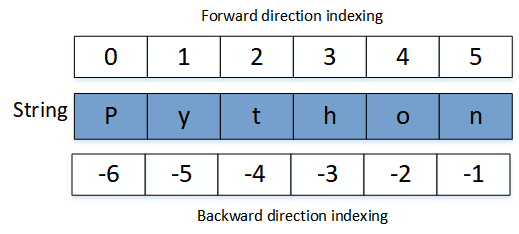
Otra operación que podemos realizar a una cadena es seleccionar solamente una parte de ella. Para ello se usa la notación [inicio:fin:paso] también en el nombre de la variable que almacena la cadena, donde:
- Inicio: es el índice del primer carácter de la porción de la cadena que queremos seleccionar.
- Fin: es el índice del último carácter no incluido de la porción de la cadena que queremos seleccionar.
- Paso: indica cada cuantos caracteres seleccionamos entre las posiciones de inicio y fin.
Observación: Para imprimir el largo de un texto, puede usar el comando len.
4.4 Ejercicios
Ejercicio 01
Escriba un programa que pida al usuario que escriba su nombre, y lo salude llamándolo por su nombre.
Ingrese su nombre: Perico
Hola, PericoEjercicio 02
Escriba un programa que reciba como entrada el radio de un círculo y entregue como salida su perímetro y su área:
Ingrese el radio: 5
Perimetro: 31.4
Área: 78.5Ejercicio 03
Escriba un programa que calcule el promedio de 4 notas ingresadas por el usuario:
Primera nota: 55
Segunda nota: 71
Tercera nota: 46
Cuarta nota: 87
El promedio es: 64.75Ejercicio 04
Escriba un programa que convierta de centímetros a pulgadas. Una pulgada es igual a 2.54 centímetros.
Ingrese longitud: 45
45 cm = 17.7165 inEjercicio 05
Escriba un programa que reciba como entrada las longitudes de los dos catetos \(a\) y \(b\) de un triángulo rectángulo, y que entregue como salida el largo de la hipotenusa \(c\) del triangulo, dado por el teorema de Pitágoras: \(c^2=a^2+b^2\).
Ingrese cateto a: 7
Ingrese cateto b: 5
La hipotenusa es 8.6023252670426267Ejercicio 06
Escriba un programa que pregunte al usuario la hora actual \(t\) del reloj y un número entero de horas \(h\), que indique qué hora marcará el reloj dentro de \(h\) horas:
Hora actual: 3
Cantidad de horas: 5
En 5 horas, el reloj marcara las 8Hora actual: 21
Cantidad de horas: 8
En 5 horas, el reloj marcara las 5Ejercicio 07
Un alumno desea saber que nota necesita en el tercer certamen para aprobar un ramo.
El promedio del ramo se calcula con la siguiente formula.
\[N_C=(C_1+C_2+C_3)/3 \\ N_F=N_C⋅0.7+N_L⋅0.3\]
Donde \(N_C\) es el promedio de certámenes, \(N_L\) el promedio de laboratorio y \(N_F\) la nota final.
Escriba un programa que pregunte al usuario las notas de los dos primeros certamen y la nota de laboratorio, y muestre la nota que necesita el alumno para aprobar el ramo con nota final 60.
Ingrese nota certamen 1: 45
Ingrese nota certamen 2: 55
Ingrese nota laboratorio: 65
Necesita nota 74 en el certamen 3Ejercicio 08
Realice un programa que calcule el área de un triángulo a partir de las longitudes de sus lados.
Para calcularlo puede utilizar la fórmula de Herón:
\[ A = \sqrt{s\,(s-a)(s-b)(s-c)}, \] donde \(a\), \(b\) y \(c\) son las longitudes de cada lado y \(s=\dfrac{a+b+c}{2}\) es el semiperímetro.
Ingrese longitud de lado 1: 3
Ingrese longitud de lado 2: 4
Ingrese longitud de lado 3: 5
El área del triángulo es 6.0