Series Temporales I¶

Introducción¶

Una serie temporal es una sucesión de datos ordenados cronológicamente, con intervalos regulares o irregulares entre observaciones. Su análisis es fundamental para tareas de predicción y pronóstico, con aplicaciones en campos como la estadística, econometría, procesamiento de señales, meteorología y finanzas.

Análisis de Series Temporales¶

Para comprender el comportamiento de una serie temporal, utilizaremos Python como herramienta principal.

Descripción del Problema¶

El conjunto de datos AirPassengers.csv contiene el número mensual de pasajeros aéreos entre 1949 y 1960. En términos estadísticos, se representa como una serie temporal [ {X_t : t \in T} ] donde:

• (X_t): número total de pasajeros en el mes (t)
• (t): tiempo medido mensualmente

Esta serie equivale a un dataframe de una sola columna, cuyo índice corresponde a las fechas.

El objetivo es predecir el número de pasajeros para los próximos dos años. Antes de ajustar un modelo, se debe analizar el comportamiento de la serie y determinar cuál modelo se adapta mejor (si existe uno adecuado).

Para ello, usaremos la librería statsmodels de Python, ideal para el análisis de series de tiempo. El primer paso consiste en cargar, transformar y visualizar los datos para explorar sus patrones.

In [25]:

# librerias 
import pandas as pd
import numpy as np 
import matplotlib.pyplot as plt 
import seaborn as sns 
import statsmodels.api as sm


# graficos incrustados
sns.set_style("whitegrid")
%matplotlib inline

# parametros esteticos de seaborn
sns.set_palette("deep", desat=.6)
sns.set_context(rc={"figure.figsize": (12, 4)})

# librerias import pandas as pd import numpy as np import matplotlib.pyplot as plt import seaborn as sns import statsmodels.api as sm # graficos incrustados sns.set_style("whitegrid") %matplotlib inline # parametros esteticos de seaborn sns.set_palette("deep", desat=.6) sns.set_context(rc={"figure.figsize": (12, 4)})

In [26]:

# Cargar dataset flights
df = sns.load_dataset("flights")

# Transformar el mes a número
df["month_num"] = pd.to_datetime(df["month"], format="%b").dt.month

# Crear columna datetime combinando año y mes
df["date"] = pd.to_datetime(df["year"].astype(str) + "-" + df["month_num"].astype(str) + "-01")

# Renombrar columnas (por claridad, opcional)
df = df.rename(columns={"passengers": "passengers"}).drop(columns=["month", "month_num", "year"],axis=1)
df.head()

# Cargar dataset flights df = sns.load_dataset("flights") # Transformar el mes a número df["month_num"] = pd.to_datetime(df["month"], format="%b").dt.month # Crear columna datetime combinando año y mes df["date"] = pd.to_datetime(df["year"].astype(str) + "-" + df["month_num"].astype(str) + "-01") # Renombrar columnas (por claridad, opcional) df = df.rename(columns={"passengers": "passengers"}).drop(columns=["month", "month_num", "year"],axis=1) df.head()

Out[26]:

	passengers	date
0	112	1949-01-01
1	118	1949-02-01
2	132	1949-03-01
3	129	1949-04-01
4	121	1949-05-01

In [27]:

# resumen
df.describe()

# resumen df.describe()

Out[27]:

	passengers	date
count	144.000000	144
mean	280.298611	1954-12-16 05:00:00
min	104.000000	1949-01-01 00:00:00
25%	180.000000	1951-12-24 06:00:00
50%	265.500000	1954-12-16 12:00:00
75%	360.500000	1957-12-08 18:00:00
max	622.000000	1960-12-01 00:00:00
std	119.966317	NaN

In [28]:

# fechas
print('Fecha Inicio: {}\nFecha Fin:    {}'.format(df.date.min(),df.date.max()))

# fechas print('Fecha Inicio: {}\nFecha Fin: {}'.format(df.date.min(),df.date.max()))

Fecha Inicio: 1949-01-01 00:00:00
Fecha Fin:    1960-12-01 00:00:00

In [29]:

# formato datetime de las fechas
df['date'] = pd.to_datetime(df['date'], format='%Y-%m')

# dejar en formato ts
y = df.set_index('date').resample('ME').mean()

y.head()

# formato datetime de las fechas df['date'] = pd.to_datetime(df['date'], format='%Y-%m') # dejar en formato ts y = df.set_index('date').resample('ME').mean() y.head()

Out[29]:

	passengers
date
1949-01-31	112.0
1949-02-28	118.0
1949-03-31	132.0
1949-04-30	129.0
1949-05-31	121.0

In [30]:

# graficar datos
y.plot(figsize=(15, 3),color = 'blue')
plt.show()

# graficar datos y.plot(figsize=(15, 3),color = 'blue') plt.show()

Se observa una tendencia creciente a lo largo del tiempo (cada año viajan más personas) y una patrón estacional marcado: los picos se repiten aproximadamente cada año, lo que indica mayor demanda en ciertos meses (como temporada alta).

Por otro lado, podemos profundizar en la comprensión de la serie temporal mediante un diagrama de cajas (boxplot) que muestre la distribución de los datos a lo largo de los distintos años.

In [31]:

# Create the boxplot
fig, ax = plt.subplots(figsize=(15, 6))
sns.boxplot(x=y.index.year, y=y["passengers"], data=y, ax=ax)

# Set labels and title
plt.xlabel("Year")
plt.ylabel("Passengers")
plt.title("Boxplot of Passengers by Year")

# Display the plot
plt.show()

# Create the boxplot fig, ax = plt.subplots(figsize=(15, 6)) sns.boxplot(x=y.index.year, y=y["passengers"], data=y, ax=ax) # Set labels and title plt.xlabel("Year") plt.ylabel("Passengers") plt.title("Boxplot of Passengers by Year") # Display the plot plt.show()

Descomposición STL¶

Una serie temporal puede descomponerse en tres componentes principales:

• Tendencia ($T$): dirección general de los datos a lo largo del tiempo (creciente o decreciente).
• Estacionalidad ($S$): fluctuaciones regulares y predecibles que se repiten en intervalos definidos (por ejemplo, cada año o cada semestre).
• Ruido ($e$): variaciones aleatorias o errores asociados a la medición o a factores no observados.

Cuando se separa la serie temporal en estas tres partes —tendencia, estacionalidad y ruido— se denomina descomposición STL (Seasonal-Trend decomposition using Loess). En algunos casos, esta descomposición no es completamente posible si la serie no presenta un comportamiento cíclico o repetitivo en el período analizado.

Existen dos enfoques principales para realizar la descomposición:

• Aditiva: $$X_{t} = T_{t} + S_{t} + e_{t}$$

• Multiplicativa: $$X_{t} = T_{t} \times S_{t} \times e_{t}$$

Aunque no es la única forma de analizar una serie temporal, esta técnica ofrece un punto de partida sólido para comprender su estructura.

En este caso, realizaremos una descomposición multiplicativa utilizando la función seasonal_decompose de la librería statsmodels.

In [32]:

from pylab import rcParams
import statsmodels.api as sm
import matplotlib.pyplot as plt

rcParams['figure.figsize'] = 18, 8
decomposition = sm.tsa.seasonal_decompose(y, model='multiplicative')
fig = decomposition.plot()
plt.show()

from pylab import rcParams import statsmodels.api as sm import matplotlib.pyplot as plt rcParams['figure.figsize'] = 18, 8 decomposition = sm.tsa.seasonal_decompose(y, model='multiplicative') fig = decomposition.plot() plt.show()

El gráfico muestra la descomposición STL de la serie temporal de pasajeros aéreos. Cada panel representa uno de los componentes principales:

1. Serie original (arriba): Muestra el número mensual de pasajeros entre 1949 y 1960. Se observa una clara tendencia creciente y un patrón estacional repetitivo cada año.

2. Tendencia (Trend): Representa el crecimiento sostenido en el número de pasajeros a lo largo del tiempo. La línea ascendente indica un aumento constante en la demanda de vuelos.

3. Estacionalidad (Seasonal): Muestra las fluctuaciones cíclicas anuales: cada año hay picos y valles que se repiten, reflejando la temporada alta y baja del transporte aéreo.

4. Residuo (Resid): Corresponde al ruido o variabilidad no explicada por la tendencia ni la estacionalidad. Se distribuye en torno a 1 (por ser una descomposición multiplicativa) y no muestra un patrón sistemático, lo que indica un buen ajuste del modelo.

Finalmente, para evaluar si el residuo obtenido se comporta como un ruido blanco, veamos cómo luce uno generado artificialmente en Python.

In [33]:

# Gráfico: Ruido blanco con distribución normal N(0,1)

import numpy as np
import matplotlib.pyplot as plt

# Fijar semilla para reproducibilidad
np.random.seed(42)

# Parámetros del ruido blanco
mean = 0       # media
std = 1        # desviación estándar
num_samples = 300  # número de observaciones

# Generar muestras aleatorias ~ N(0,1)
samples = np.random.normal(mean, std, size=num_samples)

# Visualizar la serie
plt.figure(figsize=(10, 4))
plt.plot(samples, color='steelblue', linewidth=1)
plt.title("Ruido blanco: N(0, 1)", fontsize=14)
plt.xlabel("Tiempo (t)")
plt.ylabel("Valor")
plt.grid(True, linestyle='--', alpha=0.5)
plt.show()

# Gráfico: Ruido blanco con distribución normal N(0,1) import numpy as np import matplotlib.pyplot as plt # Fijar semilla para reproducibilidad np.random.seed(42) # Parámetros del ruido blanco mean = 0 # media std = 1 # desviación estándar num_samples = 300 # número de observaciones # Generar muestras aleatorias ~ N(0,1) samples = np.random.normal(mean, std, size=num_samples) # Visualizar la serie plt.figure(figsize=(10, 4)) plt.plot(samples, color='steelblue', linewidth=1) plt.title("Ruido blanco: N(0, 1)", fontsize=14) plt.xlabel("Tiempo (t)") plt.ylabel("Valor") plt.grid(True, linestyle='--', alpha=0.5) plt.show()

El gráfico muestra un ruido blanco, es decir, una serie de valores aleatorios sin patrón. Los puntos suben y bajan sin tendencia ni repetición, oscilando alrededor de cero.

Veamos cómo se distribuyen sus valores a través de un histograma.

In [34]:

# Gráfico: Histograma del ruido blanco

plt.figure(figsize=(6, 4))
plt.hist(samples, bins=20, color='steelblue', edgecolor='black', alpha=0.7)
plt.title("Histograma del ruido blanco: N(0, 1)", fontsize=14)
plt.xlabel("Valor")
plt.ylabel("Frecuencia")
plt.grid(True, linestyle='--', alpha=0.5)
plt.show()

# Gráfico: Histograma del ruido blanco plt.figure(figsize=(6, 4)) plt.hist(samples, bins=20, color='steelblue', edgecolor='black', alpha=0.7) plt.title("Histograma del ruido blanco: N(0, 1)", fontsize=14) plt.xlabel("Valor") plt.ylabel("Frecuencia") plt.grid(True, linestyle='--', alpha=0.5) plt.show()

El gráfico muestra cómo se distribuyen los valores del ruido blanco. La mayoría se concentra cerca de 0, y pocos se alejan hacia los extremos, formando una curva en forma de campana, típica de una distribución normal.

Series Estacionarias¶

Un concepto fundamental en el análisis de series temporales es el de estacionariedad.

Definición¶

Sea $\{ X_t : t \in T \}$ una serie temporal. Se dice que la serie es débilmente estacionaria si cumple las siguientes condiciones:

• $\mathbb{V}(X_t) < \infty$, para todo $t \in T$.
• $\mu_X(t) = \mu$, es decir, su media es constante en el tiempo.
• $\gamma_X(r, s) = \gamma_X(r + h, s + h) = \gamma_X(h)$, para todo $r, s, h \in T$, lo que significa que la covarianza depende solo de la distancia entre los puntos, y no del tiempo en que se mida.

En palabras simples, una serie temporal es débilmente estacionaria cuando sus valores fluctúan alrededor de una media constante y su variabilidad no cambia a lo largo del tiempo.

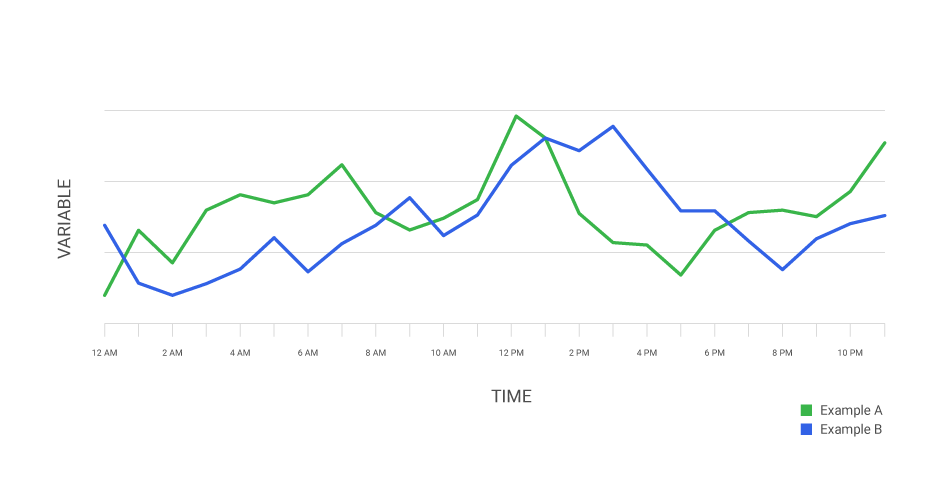
Veamos algunos ejemplos visuales:

La imagen muestra los principios de estacionariedad en una serie temporal.

• Imagen A (verde): representa una serie estacionaria, donde la media, la varianza y la covarianza se mantienen constantes en el tiempo. Los valores oscilan alrededor de una media fija con una variabilidad estable.

• Imagen B (roja): la media cambia con el tiempo (tendencia ascendente), por lo que la serie no es estacionaria.

• Imagen C (roja): la varianza cambia con el tiempo, aumentando o disminuyendo la amplitud de las oscilaciones. También es no estacionaria.

• Imagen D (roja): la covarianza cambia, lo que significa que la relación entre valores cercanos varía con el tiempo. Esta serie también es no estacionaria.

¿Por qué es importante este concepto?

• Es un supuesto fundamental en la mayoría de los modelos estadísticos de series temporales.
• Facilita el proceso de modelado y permite obtener predicciones más estables y confiables sin necesidad de transformaciones complejas.

Formas de detectar la estacionariedad¶

La forma más sencilla de evaluar la estacionariedad de una serie es observar su gráfico y analizar visualmente su comportamiento. Este método es rápido, pero depende del juicio subjetivo del observador.

Para obtener una evaluación más objetiva, existen métodos complementarios como los gráficos de autocorrelación (ACF) y autocorrelación parcial (PACF).

Definiciones básicas:

1. Función de autocorrelación (ACF): La ACF mide cuánto se parecen los valores de la serie con sus propios valores pasados. Por ejemplo, la correlación entre $X_t$ y $X_{t-1}$, entre $X_t$ y $X_{t-2}$, y así sucesivamente. En otras palabras, indica qué tan dependiente es el valor actual respecto a sus valores anteriores.

   Si la autocorrelación se mantiene alta durante muchos retardos $k$, la serie probablemente no es estacionaria, ya que conserva memoria del pasado.

2. Función de autocorrelación parcial (PACF): La PACF mide la correlación entre los valores de la serie separados por $k$ periodos, eliminando la influencia de los retardos intermedios. Esto significa que estima la relación directa entre $X_t$ y $X_{t-k}$, sin considerar los efectos de $X_{t-1}, X_{t-2}, \ldots, X_{t-(k-1)}$.

   El gráfico de la PACF permite identificar cuántos retardos tienen una influencia directa y significativa sobre el valor actual, siendo útil para determinar el orden del componente autorregresivo (AR) en un modelo.

En una serie estacionaria, los gráficos ACF y PACF muestran una disminución rápida de las correlaciones después de pocos retardos.

A continuación, graficaremos ambas funciones utilizando los comandos plot_acf y plot_pacf de statsmodels.

In [35]:

# Gráficos de autocorrelación (ACF) y autocorrelación parcial (PACF)

from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
import matplotlib.pyplot as plt

# Crear figura
plt.figure(figsize=(12, 8))

# ACF
plt.subplot(2, 1, 1)
plot_acf(y['passengers'], lags=30, ax=plt.gca())
plt.title("Función de Autocorrelación (ACF)", fontsize=12)

# PACF
plt.subplot(2, 1, 2)
plot_pacf(y['passengers'], lags=30, ax=plt.gca())
plt.title("Función de Autocorrelación Parcial (PACF)", fontsize=12)

plt.tight_layout()
plt.show()

# Gráficos de autocorrelación (ACF) y autocorrelación parcial (PACF) from statsmodels.graphics.tsaplots import plot_acf, plot_pacf import matplotlib.pyplot as plt # Crear figura plt.figure(figsize=(12, 8)) # ACF plt.subplot(2, 1, 1) plot_acf(y['passengers'], lags=30, ax=plt.gca()) plt.title("Función de Autocorrelación (ACF)", fontsize=12) # PACF plt.subplot(2, 1, 2) plot_pacf(y['passengers'], lags=30, ax=plt.gca()) plt.title("Función de Autocorrelación Parcial (PACF)", fontsize=12) plt.tight_layout() plt.show()

El gráfico muestra las funciones de autocorrelación (ACF) y autocorrelación parcial (PACF) de la serie de pasajeros aéreos.

• En la parte superior, la ACF exhibe una disminución lenta y gradual, lo que indica que los valores actuales están fuertemente relacionados con los valores pasados, incluso a grandes retardos.

  👉 Esto sugiere que la serie no es estacionaria, ya que mantiene “memoria” del pasado.

• En la parte inferior, la PACF muestra una alta correlación en los primeros retardos y luego una caída brusca.

  👉 Este patrón es típico de una serie con un componente autorregresivo (AR), donde los valores cercanos en el tiempo influyen directamente entre sí.

Prueba de Dickey-Fuller

En estadística, la prueba de Dickey-Fuller se utiliza para determinar si una serie temporal posee una raíz unitaria, es decir, si es no estacionaria. La prueba fue desarrollada en 1979 por los estadísticos David Dickey y Wayne Fuller.

Dependiendo de la versión utilizada, la hipótesis alternativa puede referirse a una serie estacionaria o tendencia-estacionaria, pero el principio general es el mismo.

Para el caso más común (verificación de estacionariedad), las hipótesis se formulan así:

• Hipótesis nula ($H_0$): la serie temporal no es estacionaria (tiene raíz unitaria).
• Hipótesis alternativa ($H_1$): la serie temporal es estacionaria.

Por lo tanto, rechazar la hipótesis nula —es decir, obtener un valor p pequeño— indica que la serie puede considerarse estacionaria.

In [36]:

# Prueba de Dickey-Fuller para verificar estacionariedad
from statsmodels.tsa.stattools import adfuller
import pandas as pd

print("📊 Resultados de la prueba de Dickey-Fuller:")

# Ejecutar el test
resultado = adfuller(y['passengers'], autolag='AIC')

# Organizar resultados principales
df_output = pd.Series(resultado[0:4],
                      index=['Estadístico de prueba', 'Valor p', '# de retardos usados', 'Número de observaciones'])

# Mostrar resultados
print(df_output)

# Interpretación rápida
if resultado[1] <= 0.05:
    print("\n✅ Se rechaza la hipótesis nula: la serie es estacionaria.")
else:
    print("\n❌ No se rechaza la hipótesis nula: la serie no es estacionaria.")

# Prueba de Dickey-Fuller para verificar estacionariedad from statsmodels.tsa.stattools import adfuller import pandas as pd print("📊 Resultados de la prueba de Dickey-Fuller:") # Ejecutar el test resultado = adfuller(y['passengers'], autolag='AIC') # Organizar resultados principales df_output = pd.Series(resultado[0:4], index=['Estadístico de prueba', 'Valor p', '# de retardos usados', 'Número de observaciones']) # Mostrar resultados print(df_output) # Interpretación rápida if resultado[1] <= 0.05: print("\n✅ Se rechaza la hipótesis nula: la serie es estacionaria.") else: print("\n❌ No se rechaza la hipótesis nula: la serie no es estacionaria.")

📊 Resultados de la prueba de Dickey-Fuller:
Estadístico de prueba        0.815369
Valor p                      0.991880
# de retardos usados        13.000000
Número de observaciones    130.000000
dtype: float64

❌ No se rechaza la hipótesis nula: la serie no es estacionaria.

¿Qué se puede hacer si la serie no es estacionaria?

En nuestro caso de estudio, la serie resultó no estacionaria. Sin embargo, existen transformaciones que pueden aplicarse para estabilizar su media y varianza, y así cumplir con las condiciones necesarias para el modelado.

Estas transformaciones deben cumplir ciertas propiedades matemáticas (como inyectividad y diferenciabilidad) para conservar la estructura de los datos. A continuación, se presentan algunas de las más utilizadas en el análisis de series temporales:

Sea $X_t$ una serie temporal, podemos definir una nueva serie $Y_t$ de la siguiente forma:

• Diferenciación: $$Y_t = \Delta X_t = X_t - X_{t-1}$$ Permite eliminar tendencias o patrones de crecimiento, reduciendo la dependencia temporal.

• Transformación de Box–Cox: $$ Y_t = \begin{cases} \dfrac{X_t^{\lambda} - 1}{\lambda}, & \text{si } \lambda \neq 0 \ \log(X_t), & \text{si } \lambda = 0 \end{cases} $$ Esta transformación estabiliza la varianza, haciendo la serie más homogénea a lo largo del tiempo.

A continuación, utilizaremos Python para visualizar cómo se comporta la serie después de aplicar estas transformaciones.

In [37]:

# Diferenciación de la serie temporal

# Aplicar la primera diferencia
Y_diff = y.diff()

# Configuración del gráfico
rcParams['figure.figsize'] = (12, 4)
plt.plot(Y_diff, color='steelblue', linewidth=1.5)
plt.title("Serie temporal diferenciada", fontsize=14)
plt.xlabel("Tiempo")
plt.ylabel("ΔXₜ = Xₜ - Xₜ₋₁")
plt.grid(True, linestyle='--', alpha=0.5)
plt.show()

# Diferenciación de la serie temporal # Aplicar la primera diferencia Y_diff = y.diff() # Configuración del gráfico rcParams['figure.figsize'] = (12, 4) plt.plot(Y_diff, color='steelblue', linewidth=1.5) plt.title("Serie temporal diferenciada", fontsize=14) plt.xlabel("Tiempo") plt.ylabel("ΔXₜ = Xₜ - Xₜ₋₁") plt.grid(True, linestyle='--', alpha=0.5) plt.show()

c:\Users\franc\AppData\Local\pypoetry\Cache\virtualenvs\docs-J5aK385Z-py3.10\lib\site-packages\IPython\core\pylabtools.py:170: UserWarning: Glyph 8348 (\N{LATIN SUBSCRIPT SMALL LETTER T}) missing from font(s) Arial.
  fig.canvas.print_figure(bytes_io, **kw)
c:\Users\franc\AppData\Local\pypoetry\Cache\virtualenvs\docs-J5aK385Z-py3.10\lib\site-packages\IPython\core\pylabtools.py:170: UserWarning: Glyph 8331 (\N{SUBSCRIPT MINUS}) missing from font(s) Arial.
  fig.canvas.print_figure(bytes_io, **kw)
c:\Users\franc\AppData\Local\pypoetry\Cache\virtualenvs\docs-J5aK385Z-py3.10\lib\site-packages\IPython\core\pylabtools.py:170: UserWarning: Glyph 8321 (\N{SUBSCRIPT ONE}) missing from font(s) Arial.
  fig.canvas.print_figure(bytes_io, **kw)

En la primera imagen, se aplica la diferenciación $$Y_t = X_t - X_{t-1}$$ Esta operación elimina la tendencia creciente de la serie original, centrándola alrededor de cero.

El resultado muestra fluctuaciones más estables en el tiempo, lo que indica que la tendencia ha sido eliminada, aunque aún puede existir cierta estacionalidad.

In [38]:

# Función para aplicar transformaciones Box-Cox
def box_transformations(y, lam):
    """
    Aplica la transformación Box-Cox a una serie temporal.
    
    Parámetros:
        y (pd.Series): serie temporal original.
        lam (float): parámetro lambda de la transformación.
        
    Retorna:
        pd.Series transformada o la serie original si λ < 0.
    """
    if lam > 0:
        return y.apply(lambda x: (x**lam - 1) / lam)
    elif lam == 0:
        return np.log(y)
    else:
        print("⚠️ El parámetro λ es negativo. Se devuelve la serie original.")
        return y

# Transformación logarítmica (λ = 0)
Y_log = box_transformations(y, 0)

# Configuración y visualización
rcParams['figure.figsize'] = (12, 4)
plt.plot(Y_log, color='darkorange', linewidth=1.5)
plt.title("Serie transformada mediante logaritmo (Box-Cox λ = 0)", fontsize=14)
plt.xlabel("Tiempo")
plt.ylabel("log(Xₜ)")
plt.grid(True, linestyle='--', alpha=0.5)
plt.show()

# Función para aplicar transformaciones Box-Cox def box_transformations(y, lam): """ Aplica la transformación Box-Cox a una serie temporal. Parámetros: y (pd.Series): serie temporal original. lam (float): parámetro lambda de la transformación. Retorna: pd.Series transformada o la serie original si λ < 0. """ if lam > 0: return y.apply(lambda x: (x**lam - 1) / lam) elif lam == 0: return np.log(y) else: print("⚠️ El parámetro λ es negativo. Se devuelve la serie original.") return y # Transformación logarítmica (λ = 0) Y_log = box_transformations(y, 0) # Configuración y visualización rcParams['figure.figsize'] = (12, 4) plt.plot(Y_log, color='darkorange', linewidth=1.5) plt.title("Serie transformada mediante logaritmo (Box-Cox λ = 0)", fontsize=14) plt.xlabel("Tiempo") plt.ylabel("log(Xₜ)") plt.grid(True, linestyle='--', alpha=0.5) plt.show()

c:\Users\franc\AppData\Local\pypoetry\Cache\virtualenvs\docs-J5aK385Z-py3.10\lib\site-packages\IPython\core\pylabtools.py:170: UserWarning: Glyph 8348 (\N{LATIN SUBSCRIPT SMALL LETTER T}) missing from font(s) Arial.
  fig.canvas.print_figure(bytes_io, **kw)

En la segunda imagen, se aplica la transformación logarítmica, equivalente al caso λ = 0 de Box–Cox: $$Y_t = \log(X_t)$$ Esta transformación reduce la amplitud de las variaciones en los valores altos, estabilizando parcialmente la varianza.

La serie conserva la tendencia ascendente, pero las oscilaciones se suavizan, lo que la hace más adecuada para el modelado.

In [39]:

# Transformación cuadrática (Box-Cox con λ = 2)

Y_quad = box_transformations(y, 2)

# Configuración y visualización
rcParams['figure.figsize'] = (12, 4)
plt.plot(Y_quad, color='seagreen', linewidth=1.5)
plt.title("Serie transformada cuadráticamente (Box-Cox λ = 2)", fontsize=14)
plt.xlabel("Tiempo")
plt.ylabel("(Xₜ² - 1) / 2")
plt.grid(True, linestyle='--', alpha=0.5)
plt.show()

# Transformación cuadrática (Box-Cox con λ = 2) Y_quad = box_transformations(y, 2) # Configuración y visualización rcParams['figure.figsize'] = (12, 4) plt.plot(Y_quad, color='seagreen', linewidth=1.5) plt.title("Serie transformada cuadráticamente (Box-Cox λ = 2)", fontsize=14) plt.xlabel("Tiempo") plt.ylabel("(Xₜ² - 1) / 2") plt.grid(True, linestyle='--', alpha=0.5) plt.show()

c:\Users\franc\AppData\Local\pypoetry\Cache\virtualenvs\docs-J5aK385Z-py3.10\lib\site-packages\IPython\core\pylabtools.py:170: UserWarning: Glyph 8348 (\N{LATIN SUBSCRIPT SMALL LETTER T}) missing from font(s) Arial.
  fig.canvas.print_figure(bytes_io, **kw)

En la tercera imagen, se usa una transformación cuadrática: $$Y_t = \dfrac{X_t^2 - 1}{2}$$ Esta amplifica las diferencias entre valores grandes y pequeños, acentuando las variaciones.

A diferencia del logaritmo, esta transformación aumenta la varianza, por lo que no es útil para estabilizar la serie, pero sirve para observar cómo cambian las propiedades estadísticas bajo distintos valores de λ.

Modelos clásicos de pronóstico¶

En esta sección se presentan los principales modelos estadísticos clásicos utilizados para el análisis y pronóstico de series temporales. La idea es avanzar desde los modelos más simples hacia los más generales, entendiendo cómo cada uno extiende al anterior.

1. Modelo de Media Móvil $MA(d)$¶

El modelo $MA(d)$ (Moving Average) describe la variable observada en el tiempo $X_t$ como una combinación lineal del ruido blanco de periodos anteriores:

$$ X_t = \mu + e_t + \theta_1 e_{t-1} + \theta_2 e_{t-2} + \dots + \theta_d e_{t-d} $$

donde:

• $e_t$ son errores aleatorios con media cero y varianza constante.
• $\theta_i$ son los coeficientes de los rezagos del error.

Interpretación: la observación actual depende de los errores pasados en el modelo.

Aplicación: útil cuando la serie es estacionaria y muestra correlación corta entre errores sucesivos.

2. Modelo Autorregresivo $AR(q)$¶

El modelo $AR(q)$ (AutoRegressive) expresa el valor actual de la serie como una combinación lineal de sus propios valores pasados:

$$ X_t = \phi_1 X_{t-1} + \phi_2 X_{t-2} + \dots + \phi_q X_{t-q} + e_t $$

donde:

• $\phi_i$ son los coeficientes autorregresivos.
• $e_t$ es un ruido blanco.

Interpretación: el valor actual depende directamente de los valores previos de la serie.

Aplicación: adecuado para series estacionarias con dependencia temporal fuerte.

3. Modelo Autorregresivo de Media Móvil $ARMA(p, q)$¶

El modelo $ARMA(p, q)$ combina las ideas de los modelos $AR$ y $MA$:

$$ X_t = \phi_1 X_{t-1} + \dots + \phi_p X_{t-p} + e_t + \theta_1 e_{t-1} + \dots + \theta_q e_{t-q} $$

Interpretación: la variable actual depende tanto de sus valores pasados como de los errores pasados.

Aplicación: se utiliza en series estacionarias que presentan tanto autocorrelación como dependencia en los errores.

4. Modelo Autorregresivo Integrado de Media Móvil $ARIMA(p, d, q)$¶

El modelo $ARIMA(p, d, q)$ extiende el modelo anterior para manejar series no estacionarias mediante la diferenciación. Si $d$ es el número de diferencias necesarias para volver estacionaria la serie, entonces:

$$ \Delta^d X_t = X_t - X_{t-1} = ARMA(p, q) $$

Interpretación: se diferencia la serie $d$ veces para eliminar tendencias o patrones no estacionarios, y luego se aplica un modelo $ARMA$.

Aplicación: series con tendencia pero sin estacionalidad marcada.

5. Modelo Estacional Autorregresivo Integrado de Media Móvil $SARIMA(p, d, q) \times (P, D, Q, S)$¶

El modelo $SARIMA$ incorpora además comportamientos estacionales en los datos, permitiendo modelar repeticiones periódicas (por ejemplo, anuales o mensuales). Su forma general es:

$$ \Phi_P (L^S) (1 - L^S)^D \phi_p (L) (1 - L)^d X_t = \Theta_Q (L^S) \theta_q (L) e_t $$

donde:

• $(p, d, q)$: parámetros no estacionales.
• $(P, D, Q, S)$: parámetros estacionales.
• $S$: período de la estacionalidad (por ejemplo, $S = 12$ para datos mensuales).

Interpretación: combina la parte no estacional del modelo ARIMA con una estructura estacional.

Aplicación: series con tendencia y estacionalidad (por ejemplo, número de pasajeros mensuales, ventas por temporada, etc.).

6. Otros modelos mencionados¶

• ARCH / GARCH: modelos para series con volatilidad variable (fluctuaciones en la varianza), comunes en datos financieros.
• Modelos de espacio de estados: generalizan los modelos anteriores para representar sistemas dinámicos complejos, donde las variables observadas dependen de variables latentes (no observadas).

Jerarquía entre modelos¶

Existe una relación jerárquica entre todos estos modelos:

$$ MA(d),\ AR(q) \subset ARMA(p, q) \subset ARIMA(p, d, q) \subset SARIMA(p, d, q) \times (P, D, Q, S) $$

Esto significa que:

• Los modelos $AR$ y $MA$ son casos particulares de $ARMA$.
• $ARMA$ es un caso particular de $ARIMA$ (cuando $d = 0$).
• $ARIMA$ es un caso particular de $SARIMA$ (cuando no hay componente estacional).

Cuándo usar cada modelo¶

Tipo de serie temporal	Modelo recomendado
Estacionaria sin estacionalidad	AR, MA o ARMA
No estacionaria (con tendencia)	ARIMA
Estacional (con patrones repetitivos)	SARIMA
Volatilidad variable (finanzas)	ARCH / GARCH
Procesos dinámicos complejos	Espacio de estados

Pronóstico con statsmodels¶

Para realizar el pronóstico utilizaremos los modelos disponibles en statsmodels, en particular el modelo $$SARIMA(p,d,q)(P,D,Q)_S.$$

Como en todo proceso de machine learning, debemos dividir los datos en dos conjuntos: entrenamiento y prueba. En el caso de las series temporales, esta división se hace según una fecha objetivo (target_date), sin alterar el orden temporal.

• $y_{train}$: todos los datos hasta la fecha target_date.
• $y_{test}$: todos los datos posteriores a target_date.

In [40]:

# Definir fecha objetivo para dividir los datos
target_date = '1958-01-01'

# Crear conjuntos de entrenamiento y prueba
y_train = y.loc[y.index < target_date]
y_test  = y.loc[y.index >= target_date]

# Visualizar ambos conjuntos
plt.figure(figsize=(10, 4))
plt.plot(y_train['passengers'], label='Entrenamiento', color='steelblue')
plt.plot(y_test['passengers'], label='Prueba', color='darkorange')
plt.title("División de la serie temporal en entrenamiento y prueba", fontsize=13)
plt.xlabel("Fecha")
plt.ylabel("Número de pasajeros")
plt.legend()
plt.grid(True, linestyle='--', alpha=0.5)
plt.show()

# Definir fecha objetivo para dividir los datos target_date = '1958-01-01' # Crear conjuntos de entrenamiento y prueba y_train = y.loc[y.index < target_date] y_test = y.loc[y.index >= target_date] # Visualizar ambos conjuntos plt.figure(figsize=(10, 4)) plt.plot(y_train['passengers'], label='Entrenamiento', color='steelblue') plt.plot(y_test['passengers'], label='Prueba', color='darkorange') plt.title("División de la serie temporal en entrenamiento y prueba", fontsize=13) plt.xlabel("Fecha") plt.ylabel("Número de pasajeros") plt.legend() plt.grid(True, linestyle='--', alpha=0.5) plt.show()

Una pregunta natural que surge es: ¿por qué no se toman los datos de forma aleatoria?

La razón es que en una serie temporal los datos están ordenados según el tiempo, por lo que existe una dependencia natural entre observaciones consecutivas. En cambio, en los problemas clásicos de regresión, cada par de datos es generalmente independiente y no sigue un orden específico.

Si seleccionáramos los datos de prueba de manera aleatoria, podríamos romper la secuencia temporal, alterando la tendencia o la estacionalidad de la serie, lo que haría que el modelo perdiera sentido.

Veamos un ejemplo sencillo de este caso en Python:

In [51]:

from statsmodels.tsa.statespace.sarimax import SARIMAX
from sklearn.metrics import mean_absolute_error, mean_squared_error
import numpy as np
import pandas as pd

def mean_absolute_percentage_error(y_true, y_pred):
    """Calcula el error porcentual absoluto medio (MAPE)."""
    y_true, y_pred = np.array(y_true), np.array(y_pred)
    return np.mean(np.abs((y_true - y_pred) / y_true)) * 100


def regression_metrics(df):
    """
    Calcula métricas de evaluación para modelos de series temporales o regresión.

    Parámetros:
        df (pd.DataFrame): DataFrame con columnas ['y', 'yhat'] donde:
            - 'y'    : valores reales
            - 'yhat' : valores predichos

    Retorna:
        pd.DataFrame: tabla con las métricas MAE, MSE, RMSE, MAPE y sMAPE
    """
    y_true = df['y']
    y_pred = df['yhat']

    mae = mean_absolute_error(y_true, y_pred)
    mse = mean_squared_error(y_true, y_pred)
    rmse = np.sqrt(mse)
    mape = mean_absolute_percentage_error(y_true, y_pred)
    smape = 2 * mape / (mape + 100)

    df_result = pd.DataFrame({
        'MAE': [round(mae, 4)],
        'MSE': [round(mse, 4)],
        'RMSE': [round(rmse, 4)],
        'MAPE': [round(mape, 4)],
        'sMAPE': [round(smape, 4)]
    })

    return df_result

from statsmodels.tsa.statespace.sarimax import SARIMAX from sklearn.metrics import mean_absolute_error, mean_squared_error import numpy as np import pandas as pd def mean_absolute_percentage_error(y_true, y_pred): """Calcula el error porcentual absoluto medio (MAPE).""" y_true, y_pred = np.array(y_true), np.array(y_pred) return np.mean(np.abs((y_true - y_pred) / y_true)) * 100 def regression_metrics(df): """ Calcula métricas de evaluación para modelos de series temporales o regresión. Parámetros: df (pd.DataFrame): DataFrame con columnas ['y', 'yhat'] donde: - 'y' : valores reales - 'yhat' : valores predichos Retorna: pd.DataFrame: tabla con las métricas MAE, MSE, RMSE, MAPE y sMAPE """ y_true = df['y'] y_pred = df['yhat'] mae = mean_absolute_error(y_true, y_pred) mse = mean_squared_error(y_true, y_pred) rmse = np.sqrt(mse) mape = mean_absolute_percentage_error(y_true, y_pred) smape = 2 * mape / (mape + 100) df_result = pd.DataFrame({ 'MAE': [round(mae, 4)], 'MSE': [round(mse, 4)], 'RMSE': [round(rmse, 4)], 'MAPE': [round(mape, 4)], 'sMAPE': [round(smape, 4)] }) return df_result

In [52]:

# Parámetros SARIMA
param = (1, 0, 0)          # (p, d, q)
seasonal_param = (0, 0, 0, 12)  # (P, D, Q, S) con S=12 (mensual)

# Asegurar que la serie tenga frecuencia temporal explícita (ajusta 'ME' o 'MS' según tu caso)
y_train_ = y_train['passengers'].asfreq('ME')
y_test_  = y_test['passengers'].asfreq('ME')

# Definir y ajustar el modelo
model = SARIMAX(
    y_train_,
    order=param,
    seasonal_order=seasonal_param,
    enforce_stationarity=False,
    enforce_invertibility=False
)
model_fit = model.fit(disp=False)

# Rango de predicción usando fechas (respeta el orden temporal)
start_index = y_test_.index.min()
end_index   = y_test_.index.max()

pred_res = model_fit.get_prediction(start=start_index, end=end_index, dynamic=False)
pred_mean = pred_res.predicted_mean
pred_ci   = pred_res.conf_int()  # intervalos de confianza

# Construir DataFrame de evaluación alineado al índice de prueba
df_temp = pd.DataFrame({
    'y':    y_test_,
    'yhat': pred_mean.reindex(y_test_.index)
})

# (Opcional) ver primeras filas
df_temp.head()

# Parámetros SARIMA param = (1, 0, 0) # (p, d, q) seasonal_param = (0, 0, 0, 12) # (P, D, Q, S) con S=12 (mensual) # Asegurar que la serie tenga frecuencia temporal explícita (ajusta 'ME' o 'MS' según tu caso) y_train_ = y_train['passengers'].asfreq('ME') y_test_ = y_test['passengers'].asfreq('ME') # Definir y ajustar el modelo model = SARIMAX( y_train_, order=param, seasonal_order=seasonal_param, enforce_stationarity=False, enforce_invertibility=False ) model_fit = model.fit(disp=False) # Rango de predicción usando fechas (respeta el orden temporal) start_index = y_test_.index.min() end_index = y_test_.index.max() pred_res = model_fit.get_prediction(start=start_index, end=end_index, dynamic=False) pred_mean = pred_res.predicted_mean pred_ci = pred_res.conf_int() # intervalos de confianza # Construir DataFrame de evaluación alineado al índice de prueba df_temp = pd.DataFrame({ 'y': y_test_, 'yhat': pred_mean.reindex(y_test_.index) }) # (Opcional) ver primeras filas df_temp.head()

Out[52]:

	y	yhat
date
1958-01-31	340.0	336.756041
1958-02-28	318.0	337.513783
1958-03-31	362.0	338.273230
1958-04-30	348.0	339.034386
1958-05-31	363.0	339.797254

In [53]:

# Resultados de las métricas del modelo
df_metrics = regression_metrics(df_temp)

# Agregar nombre descriptivo del modelo evaluado
df_metrics['Model'] = f"SARIMA_{param[0]}x{param[1]}".replace(' ', '')

# Mostrar resultados
df_metrics

# Resultados de las métricas del modelo df_metrics = regression_metrics(df_temp) # Agregar nombre descriptivo del modelo evaluado df_metrics['Model'] = f"SARIMA_{param[0]}x{param[1]}".replace(' ', '') # Mostrar resultados df_metrics

Out[53]:

	MAE	MSE	RMSE	MAPE	sMAPE	Model
0	81.8529	11619.4305	107.7935	17.0068	0.2907	SARIMA_1x0

In [54]:

# Gráfico de resultados del modelo SARIMA

plt.figure(figsize=(14, 6))
plt.plot(y['1949':], label='Observado', color='steelblue', linewidth=2)
plt.plot(df_temp['yhat'], label='Pronóstico', color='darkorange', linestyle='--', linewidth=2)

plt.title("Pronóstico de pasajeros aéreos con modelo SARIMA", fontsize=14)
plt.xlabel("Fecha")
plt.ylabel("Número de pasajeros")
plt.legend()
plt.grid(True, linestyle='--', alpha=0.5)
plt.show()

# Gráfico de resultados del modelo SARIMA plt.figure(figsize=(14, 6)) plt.plot(y['1949':], label='Observado', color='steelblue', linewidth=2) plt.plot(df_temp['yhat'], label='Pronóstico', color='darkorange', linestyle='--', linewidth=2) plt.title("Pronóstico de pasajeros aéreos con modelo SARIMA", fontsize=14) plt.xlabel("Fecha") plt.ylabel("Número de pasajeros") plt.legend() plt.grid(True, linestyle='--', alpha=0.5) plt.show()

El gráfico muestra el pronóstico del número de pasajeros usando un modelo SARIMA.

• La línea azul representa los valores observados.
• La línea naranja discontinua muestra el pronóstico generado por el modelo.

El modelo capta la tendencia creciente de la serie, pero no reproduce bien la estacionalidad, por lo que el pronóstico se ve más suavizado respecto a los datos reales.

Ahora, ¿cómo podemos hacerlo? El primer paso es definir una clase llamada SarimaModels que automatice todo el proceso anterior: ajuste, predicción y evaluación del modelo. De esta forma, podremos comparar distintos conjuntos de parámetros y seleccionar aquel que minimice las métricas de error, como MAE (error absoluto medio) y MAPE (error porcentual medio).

In [55]:

# creando clase SarimaModels

class SarimaModels:
    def __init__(self,params):

        self.params = params
        
        
    @property
    def name_model(self):
        return f"SARIMA_{self.params[0]}X{self.params[1]}".replace(' ','')
    
    @staticmethod
    def test_train_model(y,date):
        mask_ds = y.index < date

        y_train = y[mask_ds]
        y_test = y[~mask_ds]        
        
        return y_train, y_test
    
    def fit_model(self,y,date):
        y_train, y_test = self.test_train_model(y,date )
        model = SARIMAX(y_train,
                        order=self.params[0],
                        seasonal_order=self.params[1],
                        enforce_stationarity=False,
                        enforce_invertibility=False)
        
        model_fit = model.fit(disp=0)

        return model_fit
    
    def df_testig(self,y,date):
        y_train, y_test = self.test_train_model(y,date )
        model = SARIMAX(y_train,
                        order=self.params[0],
                        seasonal_order=self.params[1],
                        enforce_stationarity=False,
                        enforce_invertibility=False)
        
        model_fit = model.fit(disp=0)
        
        start_index = y_test.index.min()
        end_index = y_test.index.max()

        preds = model_fit.get_prediction(start=start_index,end=end_index, dynamic=False)
        df_temp = pd.DataFrame(
            {
                'y':y_test['passengers'],
                'yhat': preds.predicted_mean
            }
        )
        
        return df_temp
    
    def metrics(self,y,date):
        df_temp = self.df_testig(y,date)
        df_metrics = regression_metrics(df_temp)
        df_metrics['model'] = self.name_model
        
        return df_metrics

# creando clase SarimaModels class SarimaModels: def __init__(self,params): self.params = params @property def name_model(self): return f"SARIMA_{self.params[0]}X{self.params[1]}".replace(' ','') @staticmethod def test_train_model(y,date): mask_ds = y.index < date y_train = y[mask_ds] y_test = y[~mask_ds] return y_train, y_test def fit_model(self,y,date): y_train, y_test = self.test_train_model(y,date ) model = SARIMAX(y_train, order=self.params[0], seasonal_order=self.params[1], enforce_stationarity=False, enforce_invertibility=False) model_fit = model.fit(disp=0) return model_fit def df_testig(self,y,date): y_train, y_test = self.test_train_model(y,date ) model = SARIMAX(y_train, order=self.params[0], seasonal_order=self.params[1], enforce_stationarity=False, enforce_invertibility=False) model_fit = model.fit(disp=0) start_index = y_test.index.min() end_index = y_test.index.max() preds = model_fit.get_prediction(start=start_index,end=end_index, dynamic=False) df_temp = pd.DataFrame( { 'y':y_test['passengers'], 'yhat': preds.predicted_mean } ) return df_temp def metrics(self,y,date): df_temp = self.df_testig(y,date) df_metrics = regression_metrics(df_temp) df_metrics['model'] = self.name_model return df_metrics

In [56]:

# definir parametros 

import itertools

p = d = q = range(0, 2)
pdq = list(itertools.product(p, d, q))
seasonal_pdq = [(x[0], x[1], x[2], 12) for x in list(itertools.product(p, d, q))]

params = list(itertools.product(pdq,seasonal_pdq))
target_date = '1958-01-01'

# definir parametros import itertools p = d = q = range(0, 2) pdq = list(itertools.product(p, d, q)) seasonal_pdq = [(x[0], x[1], x[2], 12) for x in list(itertools.product(p, d, q))] params = list(itertools.product(pdq,seasonal_pdq)) target_date = '1958-01-01'

In [57]:

# iterar para los distintos escenarios

frames = []
for param in params:
    try:
        sarima_model = SarimaModels(param)
        df_metrics = sarima_model.metrics(y,target_date)
        frames.append(df_metrics)
    except:
        pass

# iterar para los distintos escenarios frames = [] for param in params: try: sarima_model = SarimaModels(param) df_metrics = sarima_model.metrics(y,target_date) frames.append(df_metrics) except: pass

In [60]:

# juntar resultados de las métricas y comparar
df_metrics_result = pd.concat(frames)
df_metrics_result.sort_values(['MAE','MAPE'])

# juntar resultados de las métricas y comparar df_metrics_result = pd.concat(frames) df_metrics_result.sort_values(['MAE','MAPE'])

Out[60]:

	MAE	MSE	RMSE	MAPE	sMAPE	model
0	16.4272	406.5114	20.1621	4.1002	0.0788	SARIMA_(0,1,0)X(1,0,0,12)
0	17.7173	469.8340	21.6757	4.2001	0.0806	SARIMA_(0,1,1)X(1,1,1,12)
0	17.7204	480.9764	21.9312	4.1431	0.0796	SARIMA_(1,1,0)X(1,1,1,12)
0	17.8053	501.0603	22.3844	4.1164	0.0791	SARIMA_(1,1,1)X(0,1,0,12)
0	17.8056	505.4167	22.4815	4.1061	0.0789	SARIMA_(0,1,0)X(0,1,0,12)
...	...	...	...	...	...	...
0	94.9444	14674.5556	121.1386	19.8867	0.3318	SARIMA_(0,1,0)X(0,0,0,12)
0	360.7115	150709.0664	388.2127	82.0329	0.9013	SARIMA_(0,0,1)X(0,0,1,12)
0	366.5303	153175.7993	391.3768	83.7030	0.9113	SARIMA_(0,0,0)X(0,0,1,12)
0	422.9626	187068.9748	432.5147	98.3713	0.9918	SARIMA_(0,0,1)X(0,0,0,12)
0	428.5000	189730.5556	435.5807	100.0000	1.0000	SARIMA_(0,0,0)X(0,0,0,12)

64 rows × 6 columns

En este caso, el mejor desempeño lo obtiene el modelo $SARIMA(0,1,0)\times(1,0,0,12)$. Veamos en el siguiente gráfico cómo se ajusta este modelo a los datos observados.

In [ ]:

# Ajustar mejor modelo (manteniendo tu interfaz)

param = [(0,1,0),(1,0,0,12)]
sarima_model =  SarimaModels(param)
model_fit = sarima_model.fit_model(y,target_date)
best_model = sarima_model.df_testig(y,target_date)
best_model.head()

# Ajustar mejor modelo (manteniendo tu interfaz) param = [(0,1,0),(1,0,0,12)] sarima_model = SarimaModels(param) model_fit = sarima_model.fit_model(y,target_date) best_model = sarima_model.df_testig(y,target_date) best_model.head()

Out[ ]:

	y	yhat
1958-01-31	340.0	345.765806
1958-02-28	318.0	330.574552
1958-03-31	362.0	390.254476
1958-04-30	348.0	381.573760
1958-05-31	363.0	389.169386

In [66]:

# Graficar el mejor modelo

# Se extraen las predicciones del modelo ajustado
preds = best_model['yhat']

# Se grafica la serie original desde 1949 en adelante
ax = y['1949':].plot(label='observed')

# Se superponen las predicciones sobre la misma figura
preds.plot(ax=ax, label='Forecast', alpha=.7, figsize=(14, 7))

# Se agregan etiquetas a los ejes
ax.set_xlabel('Date')
ax.set_ylabel('Passengers')

# Se muestra la leyenda y el gráfico final
plt.legend()
plt.show()

# Graficar el mejor modelo # Se extraen las predicciones del modelo ajustado preds = best_model['yhat'] # Se grafica la serie original desde 1949 en adelante ax = y['1949':].plot(label='observed') # Se superponen las predicciones sobre la misma figura preds.plot(ax=ax, label='Forecast', alpha=.7, figsize=(14, 7)) # Se agregan etiquetas a los ejes ax.set_xlabel('Date') ax.set_ylabel('Passengers') # Se muestra la leyenda y el gráfico final plt.legend() plt.show()

El gráfico muestra la comparación entre los valores reales (línea azul) y el pronóstico del modelo SARIMA (línea naranja). Se observa que el modelo reproduce bien la tendencia y estacionalidad de los pasajeros, aunque con ligeras diferencias en algunos picos.

Finalmente, analizamos los errores del modelo utilizando la función plot_diagnostics, que genera cuatro gráficos complementarios para evaluar el comportamiento de los residuales desde distintas perspectivas.

In [67]:

# Evaluar los errores del modelo
# La función plot_diagnostics muestra cuatro gráficos que permiten analizar los residuales
model_fit.plot_diagnostics(figsize=(16, 8))
plt.show()

# Evaluar los errores del modelo # La función plot_diagnostics muestra cuatro gráficos que permiten analizar los residuales model_fit.plot_diagnostics(figsize=(16, 8)) plt.show()

Estos cuatro gráficos son el resultado de la función plot_diagnostics() de statsmodels y permiten evaluar si los residuales del modelo SARIMA cumplen los supuestos estadísticos.

1. Residual estandarizado (arriba izquierda): Muestra los errores a lo largo del tiempo. Lo ideal es que fluctúen alrededor de cero sin mostrar patrones, lo que indica que el modelo capturó bien la estructura temporal.

2. Histograma y densidad (arriba derecha): Compara la distribución de los residuales con una normal estándar. Si ambas curvas (KDE y N(0,1)) se superponen bien, los errores pueden considerarse aproximadamente normales.

3. Gráfico Q-Q (abajo izquierda): Contrasta los cuantiles teóricos de una distribución normal con los cuantiles observados. Los puntos cercanos a la línea roja indican que los residuales siguen una distribución normal.

4. Correlograma (abajo derecha): Muestra la autocorrelación de los residuales. La ausencia de barras significativas fuera del intervalo de confianza (zona azul) indica que no queda estructura temporal por modelar.

Prophet¶

Prophet es un modelo desarrollado por el equipo Core Data Science de Facebook para el pronóstico de series temporales. Se basa en un enfoque aditivo, donde la serie se descompone en componentes de tendencia, estacionalidad (anual, semanal y diaria) y efectos especiales como feriados o eventos.

Este método destaca por su capacidad para:

• Adaptarse a tendencias no lineales.
• Manejar datos faltantes y cambios de tendencia.
• Ser robusto frente a valores atípicos.
• Ofrecer resultados confiables en series con fuerte estacionalidad y suficientes datos históricos.

Prophet es un proyecto de código abierto, disponible tanto en CRAN (R) como en PyPI (Python).

Nota: Para una descripción técnica detallada del modelo, consulte el artículo original.

In [ ]:

from prophet import Prophet

# rename 
y_train_prophet = y_train.reset_index()
y_train_prophet.columns = ["ds","y"]

y_test_prophet = y_test.reset_index()
y_test_prophet.columns = ["ds","y"]

# model
m = Prophet()
m.fit(y_train_prophet)

# forecast
future = m.make_future_dataframe(periods=365*4)
forecast = m.predict(future)[['ds', 'yhat']]
forecast.tail()

from prophet import Prophet # rename y_train_prophet = y_train.reset_index() y_train_prophet.columns = ["ds","y"] y_test_prophet = y_test.reset_index() y_test_prophet.columns = ["ds","y"] # model m = Prophet() m.fit(y_train_prophet) # forecast future = m.make_future_dataframe(periods=365*4) forecast = m.predict(future)[['ds', 'yhat']] forecast.tail()

21:30:16 - cmdstanpy - INFO - Chain [1] start processing
21:30:16 - cmdstanpy - INFO - Chain [1] done processing

Out[ ]:

	ds	yhat
1563	1961-12-26	537.016442
1564	1961-12-27	536.103087
1565	1961-12-28	534.348944
1566	1961-12-29	531.776196
1567	1961-12-30	528.429895

In [72]:

# metrics
result = y_test_prophet.merge(forecast,on = 'ds',how='inner')
regression_metrics(result)

# metrics result = y_test_prophet.merge(forecast,on = 'ds',how='inner') regression_metrics(result)

Out[72]:

	MAE	MSE	RMSE	MAPE	sMAPE
0	39.9165	2013.1444	44.8681	9.8461	0.1793

In [73]:

# Graficar las predicciones del modelo Prophet frente a los valores reales

# Se preparan las predicciones con el índice de fechas
preds = result[['ds', 'yhat']].set_index("ds")

# Serie observada y pronosticada
ax = y['1949':].plot(label='Observed', figsize=(14, 7))
preds.plot(ax=ax, label='Forecast', alpha=0.7)

# Detalles del gráfico
ax.set_xlabel('Date')
ax.set_ylabel('Passengers')
plt.legend()
plt.show()

# Graficar las predicciones del modelo Prophet frente a los valores reales # Se preparan las predicciones con el índice de fechas preds = result[['ds', 'yhat']].set_index("ds") # Serie observada y pronosticada ax = y['1949':].plot(label='Observed', figsize=(14, 7)) preds.plot(ax=ax, label='Forecast', alpha=0.7) # Detalles del gráfico ax.set_xlabel('Date') ax.set_ylabel('Passengers') plt.legend() plt.show()

El gráfico muestra el ajuste del modelo Prophet sobre la serie de pasajeros aéreos.

• La línea azul representa los valores observados (reales) de pasajeros a lo largo del tiempo.
• La línea naranja corresponde a las predicciones del modelo (yhat).

Se aprecia que Prophet captura correctamente la tendencia creciente y la estacionalidad anual de la serie, reproduciendo el patrón general de aumentos y descensos a lo largo de los años. Sin embargo, en algunos puntos se observan diferencias en los picos máximos y mínimos, lo que indica pequeñas desviaciones del modelo frente a las observaciones reales.

Conclusión¶

Este capítulo presentó una introducción práctica y accesible al análisis de series temporales, abordando desde la exploración inicial de los datos hasta la aplicación de modelos clásicos como SARIMA y modernos como Prophet.

Se mostró cómo evaluar la estacionariedad, ajustar modelos, interpretar sus métricas de error y analizar los residuales para validar la calidad del pronóstico. Aunque existen muchas otras metodologías y variantes más complejas, los modelos revisados permiten comprender los principios fundamentales del pronóstico y aplicar soluciones efectivas en una amplia gama de escenarios reales.

Referencias¶

1. A comprehensive beginner’s guide to create a Time Series Forecast (with Codes in Python and R)
2. A Gentle Introduction to SARIMA for Time Series Forecasting in Python
3. An Introductory Study on Time Series Modeling and Forecasting